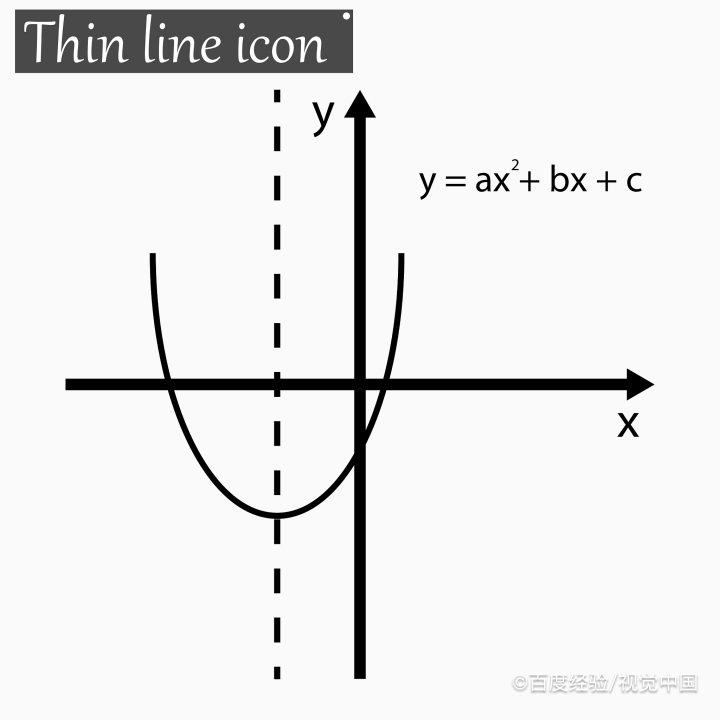
1、 问题由来,已知一个做匀加速直线运动的物体,连续通过两段长为S=1.9的位移所用的时间分别为t1=1,t2=0.9,介绍求物体加速度的几种方法步骤。

2、 首先,设前段位移的初速度为V0,加速度为a,则:前一段位移S:S屏顿幂垂=v0t1+1/2*at1^2,即:1.9=1v0+0.5锾攒揉敫a……(1)全过程位移2S:2S=V0(t1+t2)+1/2*a(t1+t2)^23.8=1.9v0+1.805a……(2)消去V0得:a =(3.8*1-1.9*1.9)/(1.805*1-0.5*1.9)=0.19/0.855=0.22m/s^2.

3、 其次,设前一段时间t1的中间时刻的瞬时速度为V1,后一段时间t2的中间时刻的瞬时速度为V2。所以:蕺清寤凯V1=s/t1=1.9/1=1.9,V2=s/t2=1.9/0.9=2.1111,又:V2=V1+a(t1/2+t2/2),即:2.1111=1.9+0.95a,所以a=(2.1111-1.9)/0.95=0.22m/s^2.

4、 第三,设前一段位移的初速度为V0,末速度为V,加速度为a。前一段S:S=V0*t1+1/2*at1^21.9=1v0+0.5a,即:v0=(1.9-0.5a)/1……(1)后一段S:S=Vt2*t2+1/2*at2^21.9=0.9Vt2+0.405a,即:vt2=(1.9-0.405a)/0.9……(2)

5、Vt2=V0+t1a,(1.9-0.405a)/0.9=(1.9-0.5a)+1a,化简有3.8/0.9-3.8/1=a(1+0.9),所以a=(4.222-0.900)/1.9=0.22m/s^2.