1、给出一个一般的3阶方阵A。

2、求出A的特征值。

3、选择任何一个特征值x,可以求出相应的特征向量X={u,v,w}:
A.X=x*X
但是,解方程的方法,显得过于笨拙了,计算机甚至解不开这个方程。
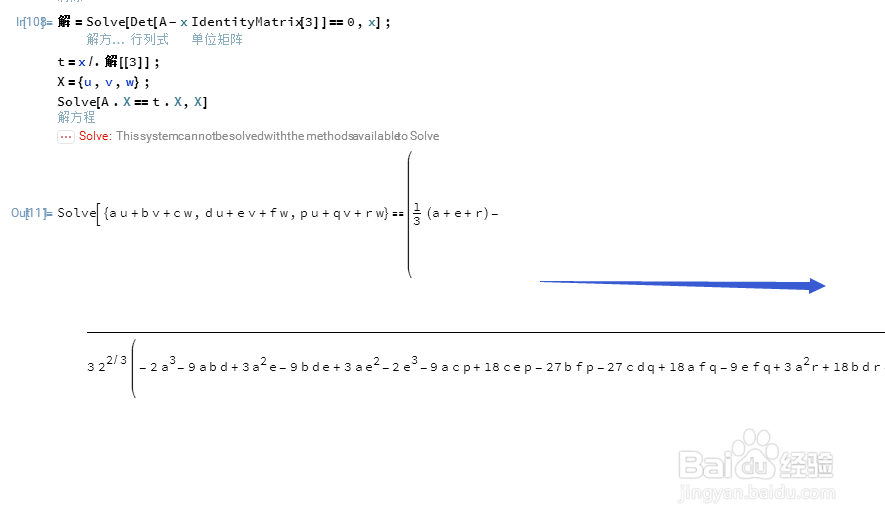
4、但是,Mathematica给出了直接计算特征向量的方法:
Eigenvectors[A]

1、下面,把A具体化:
aa={1,2,3,5,6,9,-2,3,-6};
A=Partition[aa,3];

2、Mathematica直接求出A的特征值:
Eigenvalues[A]

3、用解方程的方法,可以求出根式解。

4、Mathematica直接求特征值:
Eigenvectors[A]//Column

5、特征值和特征向量数值化:
Eigenvalues[A]//N
Eigenvectors[A]//N
