1、如果矩阵 A 是非奇异矩阵,则解 x = A\b 的大小与 b 的大小相同。例如:
A = pascal(3);
u = [3; 1; 4];
x = A\u
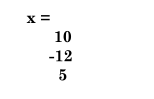
2、可以确认 A*x 恰好等于 u。
如果 A 和 b 为方阵并且大小相同,则 x= A\b 也具有相同大小:
b = magic(3);
X = A\b

3、可以确认 A*x 恰好等于 b。
以上两个示例具有确切的整数解。这是因为系数矩阵选为 pascal(3),这是满秩矩阵(非奇异的)。
1、如果矩阵 A 是非奇异矩阵,则解 x = A\b 的大小与 b 的大小相同。例如:
A = pascal(3);
u = [3; 1; 4];
x = A\u
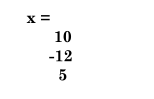
2、可以确认 A*x 恰好等于 u。
如果 A 和 b 为方阵并且大小相同,则 x= A\b 也具有相同大小:
b = magic(3);
X = A\b

3、可以确认 A*x 恰好等于 b。
以上两个示例具有确切的整数解。这是因为系数矩阵选为 pascal(3),这是满秩矩阵(非奇异的)。